Bayes' Rule

As I work through the refresher on probability and information theory, the authors showcase Bayes’ Rule which is a key statistical technique applied to e-mail filtering.

We often find ourselves in a situation where we know $P\left(y|x\right)$ and need to know $P\left(x|y\right)$. Fortunately, if we also know $P\left(x\right)$, we can compute the desired quantity using Bayes’ rule:

$$P\left(x|y\right)=\frac{P\left(x\right)P\left(y|x\right)}{P\left(y\right)}$$

Note that while $P\left(y\right)$ appears in the formula, it is usually feasible to compute

$$P\left(y\right)={\sum }_{x}P\left(y|x\right)P\left(x\right)$$

so we do not need to begin with knowledge of $P\left(y\right)$.

Excerpted from Chapter 3 of Deep Learning by Ian Goodfellow, Yoshua Bengio and Aaron Courville.

Example Code

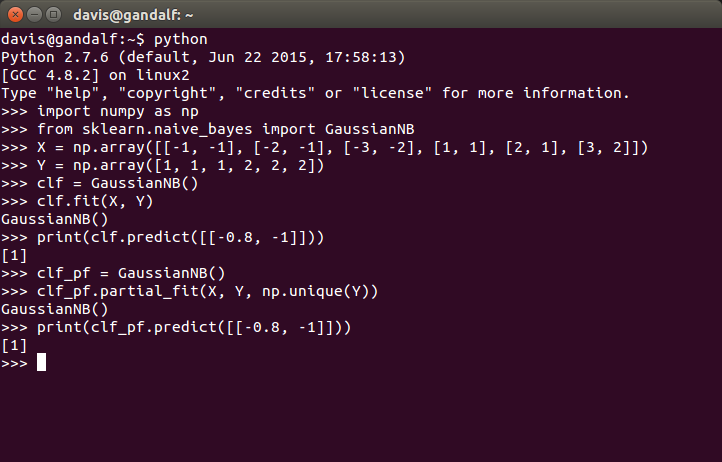
Here’s an example of prediction with a Gaussian Naive Bayes algorithm using Python’s scikit-learn library:

import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
print(clf.predict([[-0.8, -1]]))
clf_pf = GaussianNB()
clf_pf.partial_fit(X, Y, np.unique(Y))
print(clf_pf.predict([[-0.8, -1]]))

with output shown in this interactive session: